С помощта на статистиката се виждат фалшификациите на парламентарните избори в Русия, които може да се окажат спусъка на "снежна" ревюлюция.
Стандартен метод за обработка на големи масиви данни е построяването на хистограми (графики на разпределението) по различни параметри. Например при грипни епидемии медицинските статистики правят разпределение на заболеваемостта от грип по параметрите седмици и възрастови групи. За изборни резултати значим параметър е участието, т.е. процентът от избирателите, явили се на изборите. Първо, това е задължителен отчетен показател за избирателните комисии и винаги може да бъде установен и проверен. Второ, то е "чувствително" спрямо "ръчната" намеса при резултатите - ако комисията "надписва" гласовете за даден участник в изборите, то в секциите, в които става това, се увеличава и участието (там, където гласовете се отчитат точно, то не се променя).
Ето графиките на разпределението на участието в парламентарните избори в Мексико 2009, втория тур на президентските избори в Полша 2007, парламентарните избори в България 2009 и парламентарните избори в Швеция 2010. По абсцисата е нанесено участието като процент, по ординатата - броят секции. Т.е., всяка точка от кривата отразява определен брой секции с определен процент участие - примерно в 1000 секции са гласували 60% от избирателите.
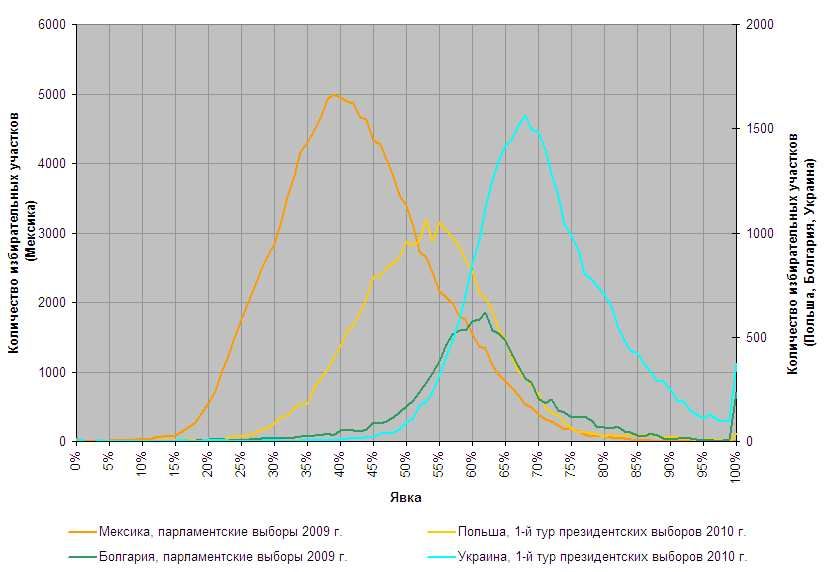
Обърнете внимание колко сходни са графиките на разпределенията в различни страни - прости, достатъчно симетрични камбановидни криви. Такива криви се получават, когато разпределението на дадена величина зависи от множество случайни независими фактори - това е известното от теорията на вероятностите нормално (или Гаусово) разпределение. Такъв вид величина е както участието в изборите, така и процентът за даден участник - тъй като всеки избирател решава дали да участва и за кого да гласува самостоятелно и независимо. Поне на теория така би трябвало да бъде и горните графики го потвърждават. Българската особеност в края на зелената крива ще коментирам накрая. Украинската има аналогичен произход на нашата.
Съвсем различни са руските криви от президентските избори 2008 и парламентарните избори 2007 и 2009:
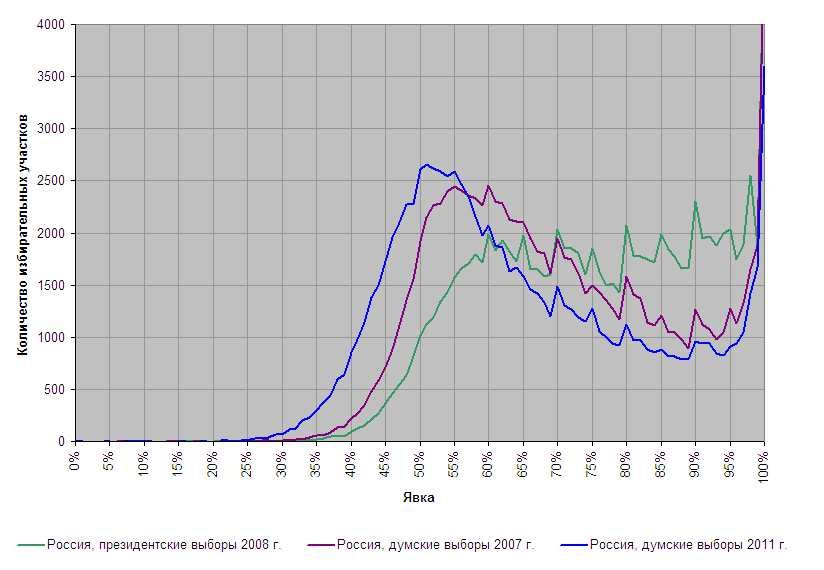
Формата е съвсем различна от камбановидната, и то най-вече при високите стойности на участие, при които разпределението не се снижава симетрично на ниските стойности, а остава високо, дори до 100% Което сочи, че най-вероятно всички тези високи стойности са "ръчни" - дело на комисията, а не на гласоподавателите. Въпреки това ще допусна, че руският гласоподавател е безаналогов гласоподавател и това, което важи за гласоподавателите по целия друг свят, не важи за него. Но дори тази хипотеза не обяснява странните пикове на кръгли стойности - на графиката се виждат отчетливи върхове на 50%, 60%, 65%, 70%, 75%, 80%, 85%, 90%, 95%. Единственото разумно обяснение е, че резултатите са нагласяни от комисиите. Но не е много вероятно хиляди комисии независимо една от друга да са решили да нарушат закона, единственото обяснение е - инструкция "отгоре".
Втора част
6 коментара:
Такива криви се получават, когато разпределението на дадена величина зависи от множество случайни независими фактори - това е известното от теорията на вероятностите нормално (или Гаусово) разпределение.
От статистическа гледна точка, това изказване е абсурдно и само показва, че става въпрос за т.нар. data-mining проблем. Това, че едно разпределение е "камбановидно" не означава, че е нормално. при нормално разпределение стойнсотите по абцисата теоритично са от минус безкрайност до плюс безкрайност. При анализа, който правите, стойностите могат да будат единствено в затворения интервал 0-100.
Дейта майнинга е проблем при статистическия анализ, когато като се рови достатъчно дълго в едни данни може да се намери "статистическа" закономерност, която обаче не се основава на солидна теоритична основа.
За да бъда коректно изследването би трябвало да се направи анализ на данни за Руските избори по гоидни и от там да се вадят изводи. В случая всички графики за Русия са сходни (тук естествено може да се постави въпроса, че всички избори са проблемни) и не може да се правят изводите, които правите вие. Т.е. разликата, която се вижда между графиките за Русия и другите, които показвате е възможно да се дължат на разлики в административното деление за изборите (напр. голям брой секции в слабо населени райони, в които има малък брой избиратели, при които 100% или близка до нея избирателна активност са по-вероятни по разлини причини).
@ Боян
Любезни, абсурдното тук е вашият коментар. Ясно е, че в руална ситуация, където броят измервания е КРАЕН, а измерваната валичина е квантувана, няма как стойностите да "са от минус безкрайност до плюс безкрайност". Затвореността на интервала не променя общата аргументация.
Направете следното упражнение: постройте си мишена и стреляйте 100 пъти по нея. Отчетете разстоянията от попаденията до центъра. Получихте ли нормално разпределение? А попадения в безкрайността имаше ли? Сега повторете с 10 изстрела. Графиката може би се различава от камбанката на Гаус? И все пак би било налудно да градим хипотеза, че в единия и другия случай действат различни закони и причинно-следствени връзки.
Така, значи при честните избори се получава по-гладка крива, а при фалшифицираните - изпъкват кръгли стойности. Кое тук не е ясно? Ми вземете анализирайте тогава, съпоставете и с резултатите от изборите преди 1989. 100% гласували (за ОФ) - какво ли ще каже статистиката, дали са повлияли някакви незвестни за науката фактори, или просто става въпрос за тоталитарна държава?
Ако още не ви е ясно, повторете горния експеримент, този път с повече стрелци и голям награден фонд. На половината вие отчитайте попаденията, а другата половина оставете сами да си отчитат. Нанесете резултатите и анализирайте графиките. Изплатете наградата. Анализирайте пак. Сравнете с хипотезата за фалшифицираните избори. Помислете колко плащаме дори и ние заради фалшифицирани резултати в Русия.
@ Анонимен
Любезни, надявам се осъзнавате, че примера, който давате не отговаря на ситуацията с изборите.Първо, стрелбата сама по себе си не е случайно събитие. Но ако приемем, че сте се прицелили с абсолютна точност и единствено атмосферните условия са внесли случаен елемент, то във вашия пример със стрелбата, става дума за извадка от 100 изстрела от съвкупност (всички възможни изстрели), която има нормално рапределение. И да, коклкото и да не ви се вярва, при стрелбата (приемаме, че тя е случайно събитие) възможните отклонения теоритично са от минус безкрайност до плюс безкрайност (т.е. винаги е възможно още един микрон отклонение). В изследването на изборите имаш наблюдения върху цялата съвкупност и не е възможно да имаш стойности извън затворения интервал 0-100.
колкото до пиковете на кръглиоте стойности - не ви ли се струва леко абсурдно, ако някой фалшифицира избори, да направи избирателната активност във фалшифицираните протоколи такива "кръгли стойности". По-скоро би ги избягвал...
Друг анонимен съм.
При всички случай независимо от дискретните стойности функцията на разпраделение трябва да е "гладка" - или с други думи казано със слабо различаващи се стойности за съседни отчети.
Преди години за един "конкурсен" изпит, за който имах лични интереси от резултата ми направи впечатление голямата разлика в успеха между последния приет и първия неприет. В реални конкурси с голям брой участници - СУ, ТУ-София и прочее той е през всички години една-две стотни.
Няма да казвам къде беше при 4000 участници за 200 места 35 стотни.
По въпроса - математическата статистика и теорията на вероятностите са част от науката, и понеже имам два три изпита, свързани с нея за големи числа очаквам гладки функции. Там, където производната е голяма очевидно е внесена енергия отвън, когато става дума за разпределение на физическа величина. Eто точно тази енергия се коментира в поста и той си заслужава времето за прочит.
Реалните физически процеси НИКОГА не дават безкрайни резултати. Колкото и да стреляш, абсолютно никога няма да имаш безкрайно отклонение. ТеорИтично може (математиката не забранява), но на практика е забранено от законите на физиката. Никой статистически метод не е бил прилаган, никога, върху безкраен масив от данни ("всички възможни"). В практиката, ако в данните се появят безкрайности, значи има груба грешка.
В социологическата статистика интервалът винаги е затворен и най-често квантуван до цели числа.
Абсурдно е да се опитваш да опровергаеш явното (изборите в Русия се фалшифицират) с теорИтични философски разсъждения, маскирани като статистика.
От друга страна, точно такива резултати се получават, когато накараш хората да изпълнява идиотски поръчения. "Трябва да имате активност от 70% / 80% / 90%". Изпълнено, резултатите са налице. Петилетката за 4 години. 100% за ОФ.
Ама сте ми палета - бързате с теоретичните коментари преди авторката да е развила докрай идеята си.
@Боян - не издребнявай за нормалното разпределение де, Вени просто не е „начертала графиката“ наляво от нулата и надясно от 100. ;) От друга страна изречението, започващо с „Дейта майнинга е проблем ...“ е ебаси простотията, да ме извиняваш за неакадемичния тон. Data mining не е проблем, а, грубо казано, е процес за издирване на неявни закономерности. Уточнение - статистическите закономерности са около границата явно-неявно, като поне (!!!) популярната част от тях са от страната на явното. Мога да продължа нататък, но не му е времето и мястото.
По темата - като видим всички части ;)
Публикуване на коментар